当前位置：首页>>广州有道有限元>>ANSYS有限元分析
ANSYS 粘弹性材料
1.1 ANSYS中表征粘弹性属性问题
粘弹性材料的应力响应包括弹性部分和粘性部分，在载荷作用下弹性部分是即时响应的，而粘性部分需要经过一段时间才能表现出来。一般的，应力函数是由积分形式给出的，在小应变理论下，各向同性的粘弹性本构方程可以写成如下形式：
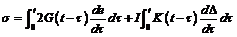(1)
其中
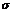＝Cauchy应力
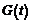＝为剪切松弛核函数
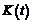＝为体积松弛核函数
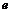＝为应变偏量部分（剪切变形）
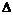＝为应变体积部分（体积变形）
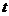＝当前时间
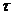＝过去时间
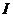＝为单位张量。
该式是根据松弛条件本构方程(1)，通过将一点的应变分解为应变球张量（体积变形）和应变斜张量（剪切变形）两部分，推导而得的。这里不再敖述，可参考相关文献等。
ANSYS中描述粘弹性积分核函数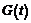
和
参数表示方式主要有两种，一种是广义Maxwell单元（VISCO88 和 VISCO89）所采用的Maxwell形式，一种是结构单元所采用的Prony级数形式。实际上，这两种表示方式是一致的，只是具体数学表达式有一点点不同。1.2 Prony级数形式
用Prony级数表示粘弹性属性的基本形式为：
(2)
(3)
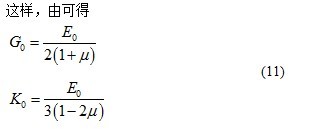
1.3 Shift Function：
Shift function (转换函数)
有三项可以选择：
(a) William-Landel, ferry: 时温等效方程, 适用于聚合体
Tref: 即理论中的C1-Relative temperature: 相对温度（对应《粘弹性理论》中的时温等效方程（WFL方程）应该是玻璃化转变温度）
C1,C2: WFL方程的常量，与材料有关；
（b） Tool-Narayanaswamy 方程
Tref: 理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）
C1: 就是TN常量；
(c) 用户定义
Tref: 理论中的C1-Relative temperature: 相对温度（应该是玻璃化转变温度）
C1: 方程的常量；
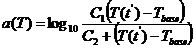
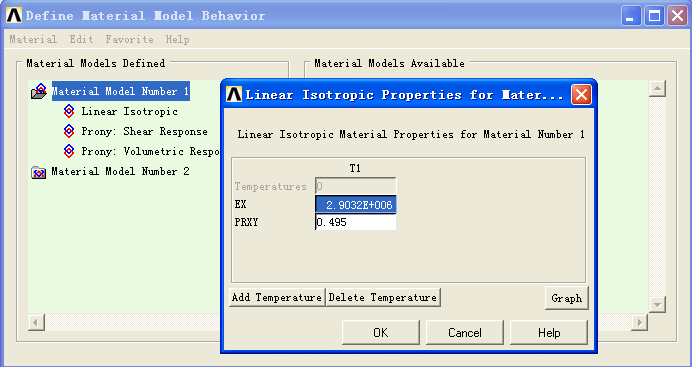
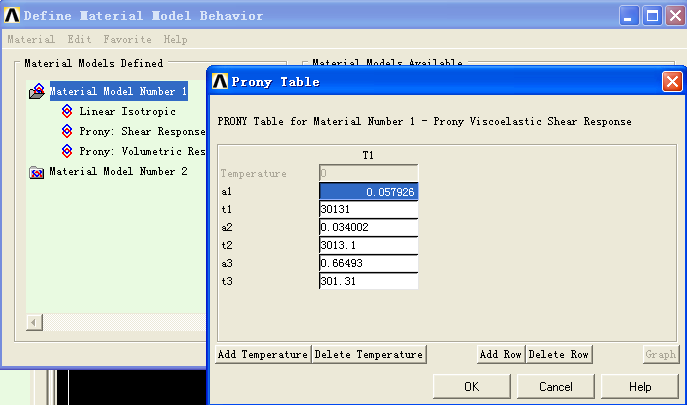
在使用PRONY模拟时，SHIFT FUNCTION不是一定要输入的，如果松弛模量E(t)与温度不相关，可以不用输入shift function.
参数输入情况分别如下图所示：
